Izrādās, pa līkumu iet ir ātrāk! To arī šodien apskatīsim. (Starp citu, sveicieni Lieldienās!)
Pa līkumu, kā izrādās, iet ir ātrāk... nu labi, šļūkt. Pie tā mēs vēl... atgriezīsimies.
Izrādās, pa līkumu iet ir ātrāk! To arī šodien apskatīsim. (Starp citu, sveicieni Lieldienās!)
Pa līkumu, kā izrādās, iet ir ātrāk... nu labi, šļūkt. Pie tā mēs vēl... atgriezīsimies.
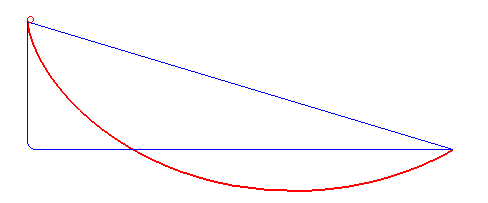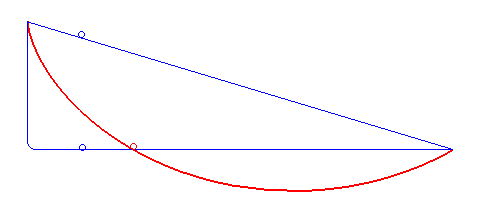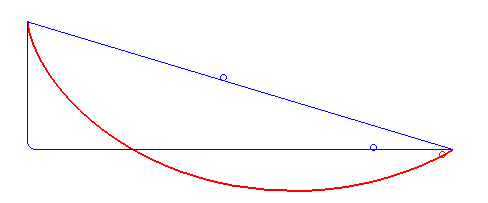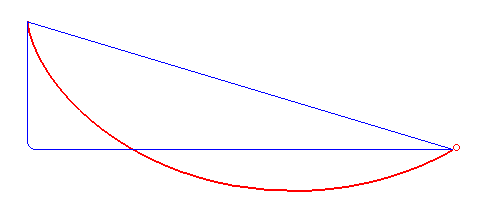
Šajā GIFā ir redzamas bumbiņas, kas krīt no taisnas līnijas, pa līniju, kura iet sākumā taisni uz leju, samērā ātri kļūst par horizontālu, un pēc tam beidzas, un mūsu izliektā līnija. Pa to, kā redzams, bumbiņa krīt visātrāk.
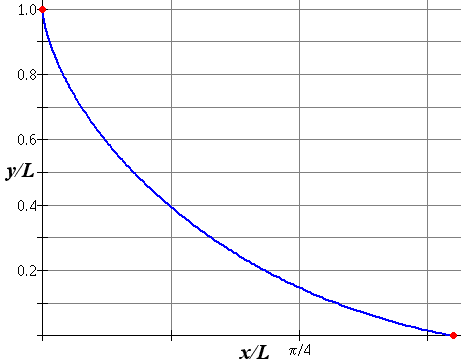
Es varētu iekļaut matemātiku, kā tas darbojas, bet šaubos, vai jūs tas interesētu, tāpēc nē.
Vēl viens interesants fakts - lai kur bumbiņu uzliktu uz līknes, tā aizripos vienādā laikā. To droši vien nevar saprast tā pa taisno, bet ar to es domāju tā - ja mums ir divas vienādas šādas līknes, un vienu bumbiņu mēs sākam ripināt pašā augšā, bet otru - teiksim, no vidus, abas bumbiņas līdz galam nonāks vienādā laika sprīdī. Tas ir tik dīvaini!
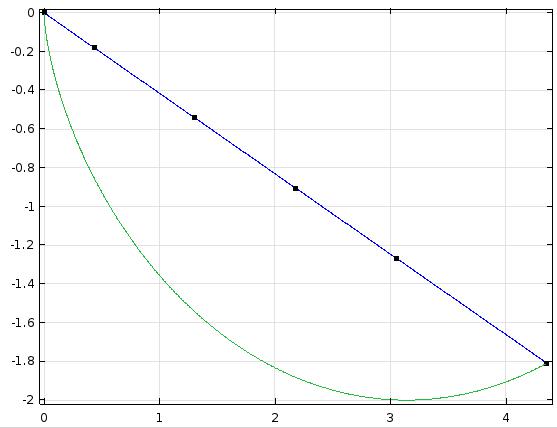
Vēl viens fakts: ja mēs paņemam apli, teiksim, izgrieztu no koka, un to ripinām guļus uz papīra, bet pie malas piestiprinām zīmuli, ripinoties šis zīmulis zīmēs mums jau pazīstamo līkni. Tas ir dīvaini, tomēr, ripinot lieldienu olas, līkni zīmēt neizdosies, jo ola ir ovāla, nevis apaļa.
Kāpēc tieši pa līkni ripināt bumbu ir visātrāk?
Johans un Jakobs Bernulli katrs piedāvāja savu versiju. Johans pielietoja matemātiku un Fermā principu, taču viņa brālis Jakobs parādīja, kā divi diferenciāļi var izveidot formu, pa kuru ripinot bumbu var aizņemt mazāk laika.

Atceraties, raksta sākumā teicu, ka pie šļūkšanas atgriezīsimies? Ar to domāju akvaparka caurules! Tās caurules, skatoties no augšas, ir visādi izkropļotas, lai interesantāk... taču, ja tādi virpuļojumi nebūtu, tad, no sāniem skatoties... var redzēt mūsu pazīstamo līkni! Nu gan gudri pastrādājuši, jo, ja šādas līknes nebūtu, mēs pa to neslīdētu tik ātri... nu, jūs, jo es tur nekad neesmu bijis... ![]()
Ceru, ka jums patika! Esiet godīgi, ja labs raksts, tad pluss, ja slikts raksts, tad mīnuss.

pluss, bet īsti nepabeigts raksts.. stipri saraustīts ![]()
un vel , virsraksts, nevis iet bet krist, ripot, šļūkt,
jo parasti ar iet saprot pārvietošnos horizontālā plaknē, nevis vertikālā
"Es varētu iekļaut matemātiku, kā tas darbojas, bet šaubos, vai jūs tas interesētu, tāpēc nē."
Kāpēc? Es gribu redzēt arī to matemātiku. Citādi nesaprotu ![]()
Autoram gravitācija vienmēr palīdz uzvarēt Pitagoru, parkā izvēloties trajektoriju? ![]()