Par cik mūsdienās daudzi vēlas savu karjeru saistīt ar grafikas veidošanu, apstrādi. Tad nolēmu izveidot rakstu, kurš ir atvasināts no pilnlauku matemātikas, ko varētu saistīt ar loģikas distanci, kur pārklājot šķeltus, bezgalīgi aizpildītus laukus ir iespējams iegūt noteiktas formas plaknē. Ja pilnlauku matemātika tiek uzskatīta par manipulēšanu ar bezgalīgi aizpildītiem laukiem, tad šķeltlauku apstrādi var iztēloties, kā apgrieztu lauku bezgalīgi aizpildītam, šķeltam laukam. Citiem vārdiem sakot šķeltlauku apstrādē tiek izslēgti bezgalīgi aizpildīti lauki, tos aizstājot ar begalīgā, šķeltā lauka apgrieztu lauku.
Kas kopējs pilnlauku matemātikai un šķletlauku apstrādei:
+ sagalbājas sistēmas lauks
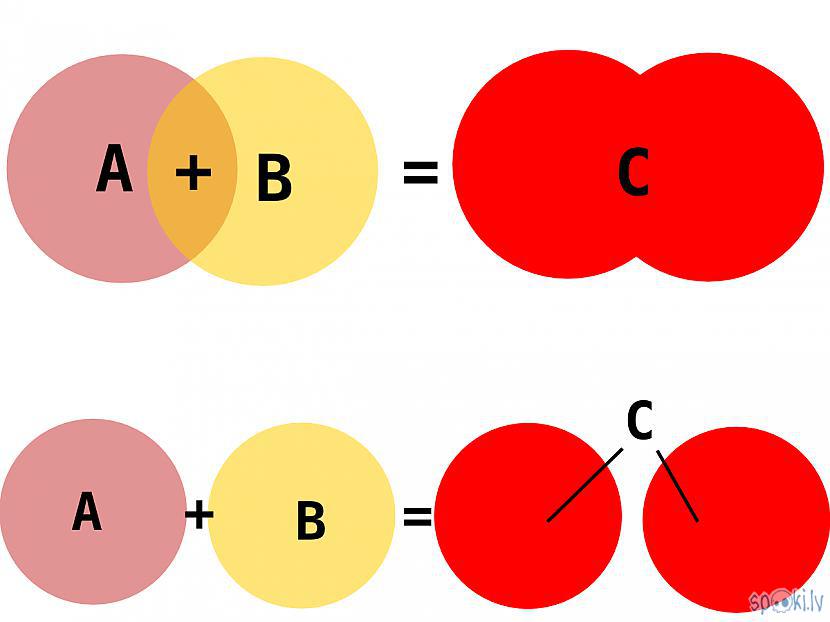
+ sagalbājas lauku saskaitīšanas metode
Kas atšķirīgs pilnlauku matemātikai un šķeltlauku apstrādei:
- šķeltlauku apstrādē nedrīkst pielietot reizināšanu
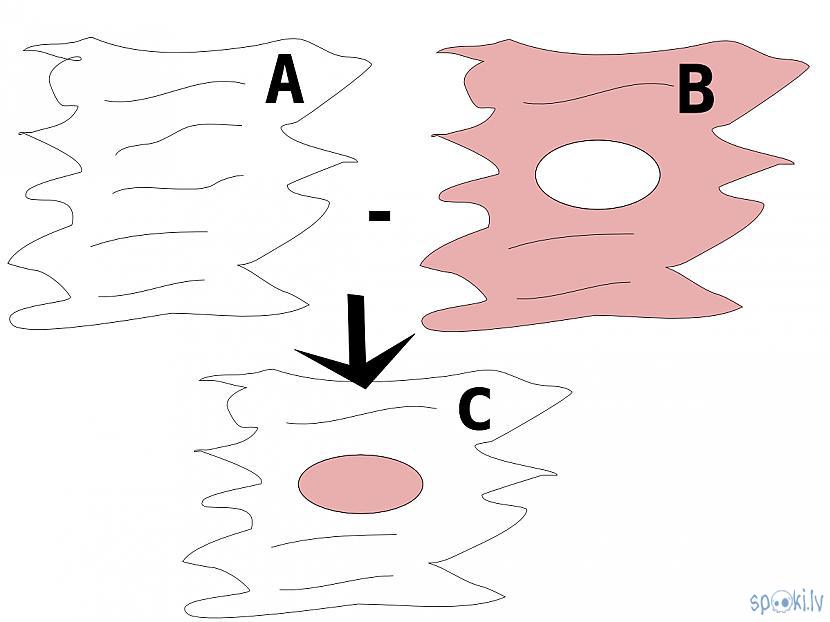
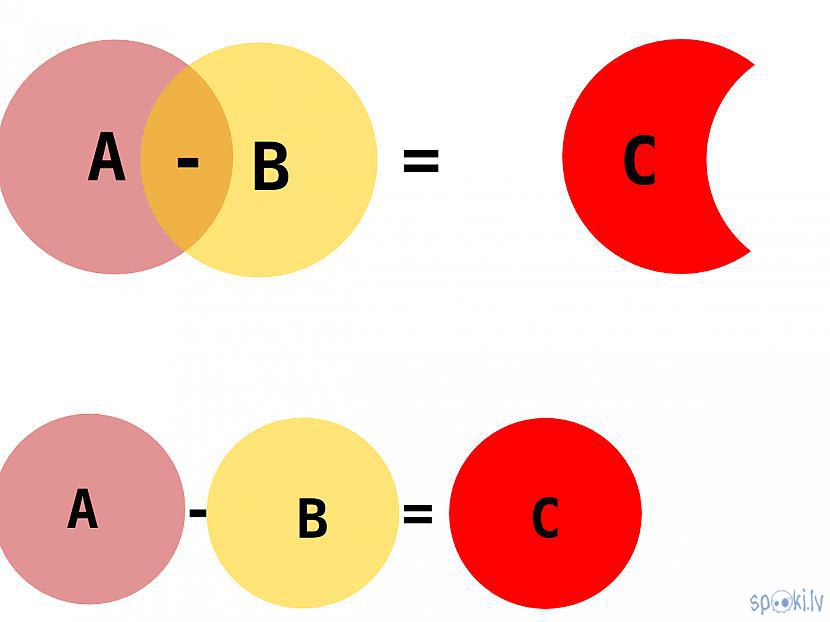
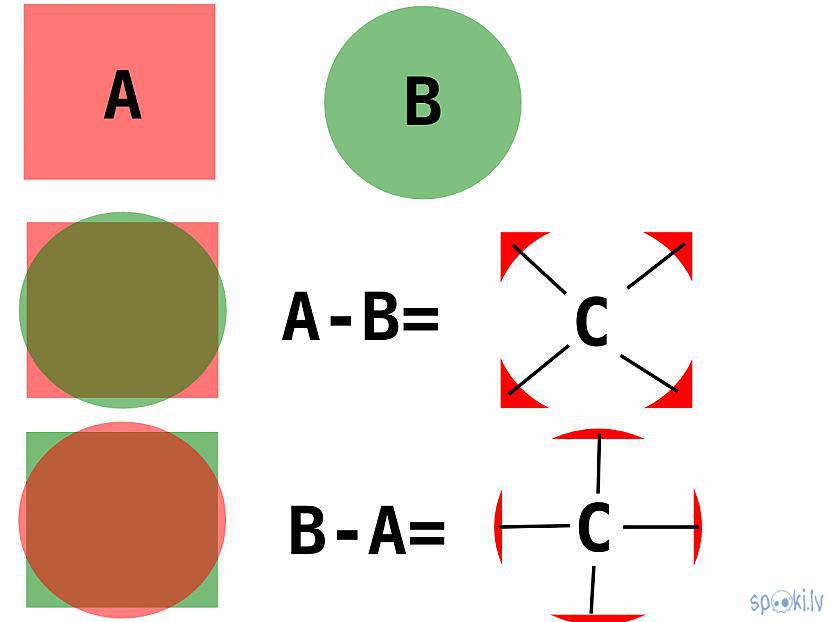
- atņemšanā nozīme ir arī lauku secībai vai svarīgs ir lauks no kura tiek atņemts cits lauks
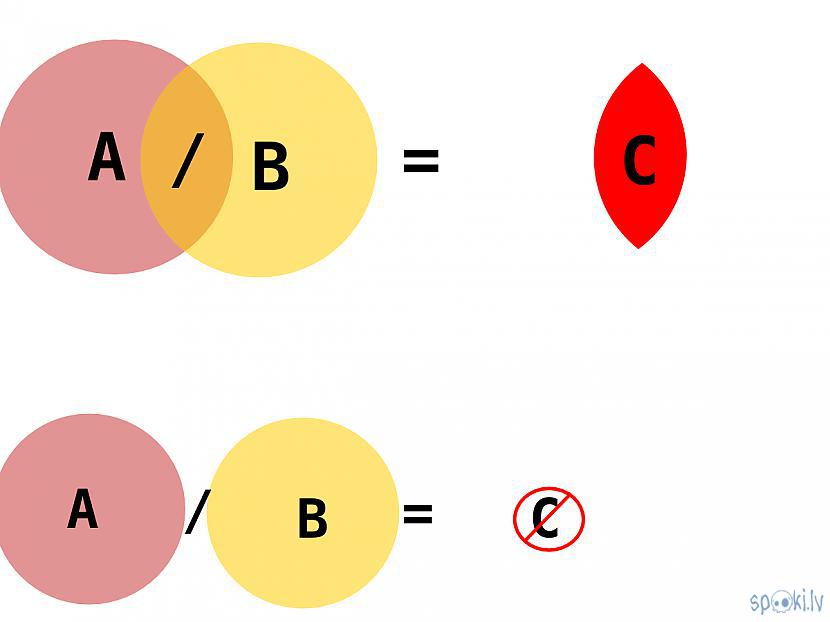
- dalīšanā var vien iesaistīt divus ierobežotus laukus
- katrā darbībā vien var iesaistīt divus laukus, pēc tam iegūstot vēlamo lauku ir iespējams to pakļaut citai darbībai
- visi darbībās izmantotie lauki ir ierobežoti sistēmas laukā, tie nevar būt bezgalīgi
Šķeltlauku darbības, kuras ir atšķirīgas no pilnlauku matemātikas darbībām:
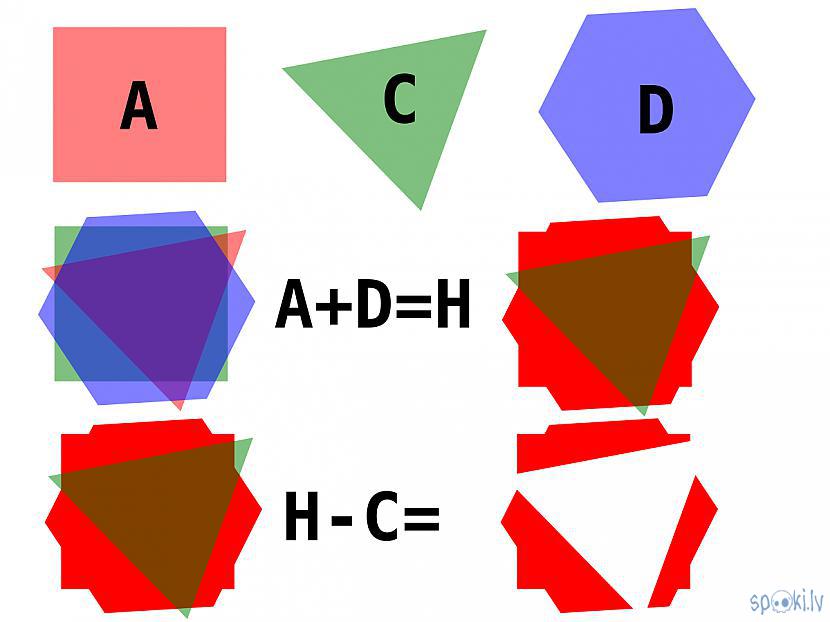
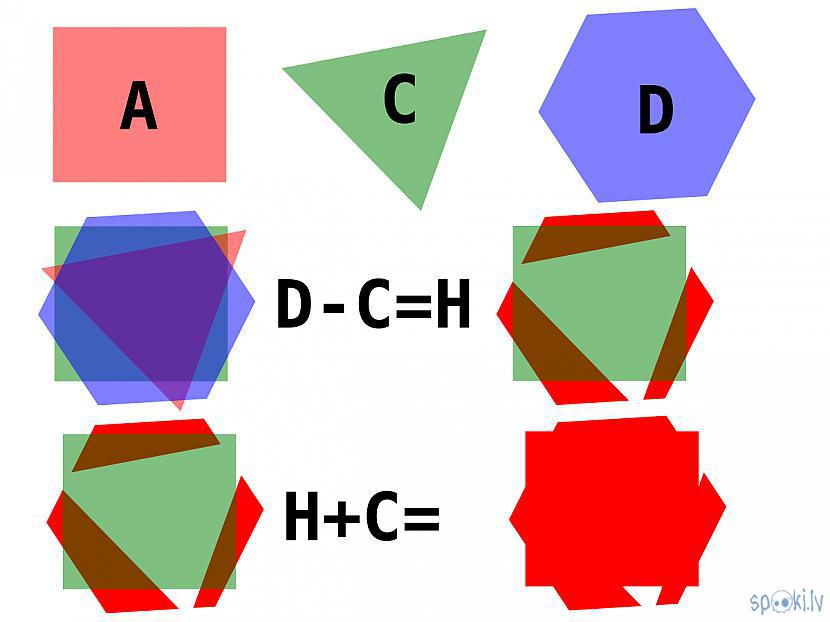
o saskaitīšana ir divu lauku apvienošana, kas arī veido ierobežotu lauku
o atņemšana ir ierobežotu lauku pārpalikuma iegūšana, ja lauki savā strapā nepārklājas pirms darbības veikšanas, tad ar atņemšanu tiek izslēgts atņemamais lauks no sistēmas lauka.
o dalīšana ir divu ierobežotu lauku pārklājuma iegūšana, ja lauki savā starpā nepārklājas, tad no sistēmas lauka tiek izslēgs gan dalāmais lauks, gan dalīšanā izmantojamais lauks
Svarīgākais izmantojot šķeltlaukus ir saprast, ka visas sev vēlamās formas ir iespējams iegūt, izmantojot vien saskaitīšanu, atņemšanu vai dalīšanu. Dalīšana un atņemšana šķeltlauku apstrādē krasi atšķiras no pilnlauku matemātikas. Vai šķeltlauku apstrādē tiek vien iesaistīti ierobežoti lauki un sistēmas laukā nedrīkst būt iekļauti bezgalīgi aizpildīti lauki, bez tam šķeltus, ierobežotus laukus sistēmas laukā var reprezentēt šķietami vairāki lauki vai lauka daļas vienlaicīgi.
lasi, vērtē, komentē ![]()